This is the Vogels-Abbott Benchmark (from Brette et al. 2007) network adapted from the examples included in PyNN. It implements a smaller version of the conductance based, self-sustained balanced network from (Vogels and Abbott (2005)).

To run the program the network first needs priming with external Poisson noise before it can self-sustain its activity. To do that invoke the program with the following command line arguments

./sim_coba_benchmark --dir /tmp --simtime 5

The prime keyword in the first command causes the network to run with external Poisson input and save its network state at the end of the run to a set of files created under /tmp. Note that you can give any other directory name where you want the files to be created. The second call to the progrem without the –prime argument causes the program to read the current network state from these saved files and runs the network for the specified period in simtime. All spiking output and the memory trace (mem file) of a single neuron are written to the directory specified with –dir and are prefixed with coba.*.

If you are interested in running the code in parallel please see the parallel execution howto.

In the above example the output is written to /tmp.

bash-4.1$ ls -l /tmp/coba.0.*
   8 -rw-r--r-- 1 zenke lcn1    5447 Jan 13 11:17 /tmp/coba.0.log
3208 -rw-r--r-- 1 zenke lcn1 3282541 Jan 13 11:17 /tmp/coba.0.e.ras
 764 -rw-r--r-- 1 zenke lcn1  780757 Jan 13 11:17 /tmp/coba.0.i.ras
 928 -rw-r--r-- 1 zenke lcn1  950019 Jan 13 11:17 /tmp/coba.0.e.mem
 916 -rw-r--r-- 1 zenke lcn1  935976 Jan 13 11:17 /tmp/coba.0.e.gaba
 880 -rw-r--r-- 1 zenke lcn1  900018 Jan 13 11:17 /tmp/coba.0.e.ampa

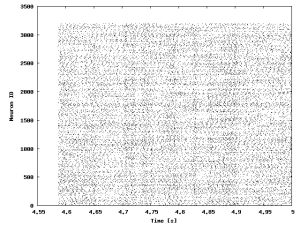This figure shows the raster plot of the spiking activity of the excitatory population written to /tmp/coba.0.e.ras.

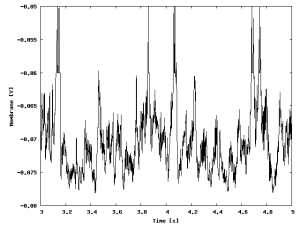The figure shows the evolution of the membrane potential of one excitatory cell during the simulation.

TIFGroup * neurons_e = new TIFGroup( ne);
TIFGroup * neurons_i = new TIFGroup( ni);
 
neurons_e->random_mem(-70e-3,10e-3);
neurons_i->random_mem(-70e-3,10e-3);

This part instantiates two groups of neurons of type TIFGroup which corresponds to the conductance based model with exponentially decaying PSCs and an absolute refractoriness of 5ms. The random_mem methods randomize the initial membrane potentials with a Gaussian (mean=-70mV and standard deviation 10mV).

The sparse random connectivity is initialized as follows:

SparseConnection * con_ee 
   = new SparseConnection( neurons_e,neurons_e, w, sparseness, GLUT);
 
SparseConnection * con_ei 
   = new SparseConection( neurons_e,neurons_i, w,sparseness,GLUT);
 
SparseConnection * con_ie 
   = new SparseConnection( neurons_i,neurons_e,wi,sparseness,GABA);
 
SparseConnection * con_ii 
   = new SparseConnection( neurons_i,neurons_i,wi,sparseness,GABA);

here w contains the synaptic weight of excitatory synapses and wi the one of their inhibitory counter part. The network has a global sparseness of 2%.

The following code snipped is responsible for running the simulation for simtime seconds. The second parameter true indicates that we wan the simulation to be interrupted if the RateChecker detects too high firing rates, which usually suggests that something is going wrong.

if (!sys->run(simtime,true)) 
    errcode = 1;
 
if ( prime ) { 
    oss.str("");
    oss << dir << "/save";
    sys->save_network_state(oss.str());
}

The second part of the above code saves the network state if prime==true and is therefore used to create the initial conditions of the self-sustained activity.