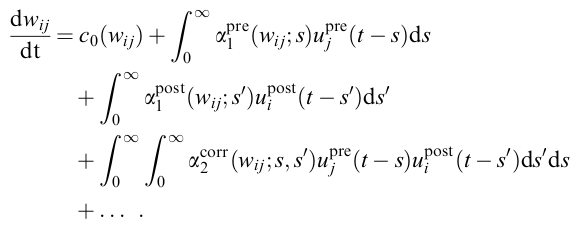Table of Contents
Synapse and Plasticity Models
Auryn was written with the aim to simplify the development of spike-timing-dependent plasticity (STDP) models and to run them efficiently in distributed network simulations. Behind the scenes Auryn diverts from existing standard simulators (like NEST) in that it has the inbuilt functionality to back-propagate action potentials to the presynaptic neurons. This largely simplifies implementing plasticity models which can be written as the product of “some synaptic quantities” and the pre- or postsynaptic spike train. For instance, most standard STDP models fall into this category. In particular the synaptic weight only changes upon the arrival of pre- or postsynaptic spikes. If you do not know what any of this means, it might be good to have a look at the following papers:
- Gerstner, W., and Kistler, W.M. (2002). Mathematical formulations of Hebbian learning. Biol Cybern 87, 404–415. full text
- Zenke, F., and Gerstner, W. (2014). Limits to high-speed simulations of spiking neural networks using general-purpose computers. Front Neuroinform 8, 76. full text
If you can write down a learning rule as a differential equation involving spike trains, synaptic traces and specific postsynaptic quantities, such as the membrane potential, Auryn will bring everything you need to implement this learning rule intuitively. Here is an example from Gerstner and Kistler (2002):
In Auryn you can implement this type of learning rule if the u can be written as a function of synaptic traces and postsynaptic quantities (for many standard cases the u are synaptic traces themselves). To that end, Auryn has native support for such pre- or postsynaptic traces. For historical reasons, I typically use the letter z for synaptic traces, which is what you will find below.
Understanding plasticity in Auryn
In most cases you will want to use Auryn to implement your own synapse model. The easiest to do this is by understanding and modifying an existing model. Most of the plasticity models in Auryn are implemented in source files which contain the acronym STDP, e.g. STDPConnection, STDPwdConnection, SymmetricSTDPConnection or “Triplet” in the case of TripletConnection which is used in this example. You will find them in the src/auryn directory, or take a look at the class index. All the classes implement SparseConnection objects with plasticity on top. They already implement all the purely virtual functions of the base class Connection and specific functions to implement plasticity. In the following, I will explain how to understand these classes and how to easily modify them according to your needs. In particular, I will cover how to define your own synaptic traces and how to use them to define weight updates. Finally, I will illustrate how synaptic weights can be integrate in a time continuous manner, for instance to implement a weight decay, homeostatic scaling or other continuous processes.
Synaptic traces
Synaptic traces in Auryn are objects that integrate the state of the following linear differential equation:
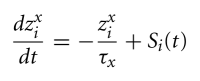 which can be understood as the exponentially decaying effect of “something” that happens at the synapse following either the pre or postsynaptic spike. Synaptic traces are characterized by their time constant
which can be understood as the exponentially decaying effect of “something” that happens at the synapse following either the pre or postsynaptic spike. Synaptic traces are characterized by their time constant tau and by whether they are a presynaptic or a postsynaptic trace. The typical declaration of one pre- and three postsynaptic traces in the header file of a plastic connection (in this case TripletConnection) looks the following:
/* Definitions of presynaptic traces */ PRE_TRACE_MODEL * tr_pre; /* Definitions of postsynaptic traces */ DEFAULT_TRACE_MODEL * tr_post; DEFAULT_TRACE_MODEL * tr_post2; DEFAULT_TRACE_MODEL * tr_post_hom;
The macros DEFAULT_TRACE_MODEL and PRE_TRACE_MODEL are defined in auryn_definitions.h to facilitate the change of the underlying integration scheme. Per default they refer to EulerTrace, because Euler integration is most efficient in most situations (see Zenke and Gerstner (2014) for details).
This declaration should be matched in the .cpp file. Typically there should be an init function in your plastic connection class in which you can write:
/* Initialization of presynaptic traces */ tr_pre = src->get_pre_trace(tau_plus); /* Initialization of postsynaptic traces */ tr_post = dst->get_post_trace(tau_minus); tr_post2 = dst->get_post_trace(tau_long); tr_post_hom = dst->get_post_trace(tau_hom);
which initializes the traces using their respective time constants tau_* and registers them to either the presynaptic (src) or the postsynaptic (dst) NeuronGroup respectively. By doing so, the traces will be automatically evolved (decay over time) and incremented by one upon each spike of the corresponding NeuronGroup. Moreover, if multiple Connection objects were to define a trace with the same time constant for the same NeuronGroup, Auryn 'knows' about this and internally only computes the trace once to speed up computation. The current value of a trace can then be accessed in the code via tr_post→get(NeuronID id) which we will use in the next section to compute weight updates.
Weight updates at spiking events (propagate)
The code described in the previous section ensures that you have a bunch of pre- and postsynaptic traces at your hands, but it does not implement any weight update. To do so you will have to implement the function propagate() which is defined as purely virtual function in Connection. For reasons of clarity it is generally a good idea to split this function logically into spike propagation (in forward direction, pre→post) and spike back-propagation. The following example shows how this is done in TripletConnection:
void TripletConnection::propagate() { propagate_forward(); propagate_backward(); }
Let's first have a look at what we have to implement in propagate_forward().
Forward spike propagation
By forward propagation we mean the actions that are triggered by a presynaptic spike postsynaptically. This includes on the one hand evoking a postsynaptic conductance, but in the case of plastic connection object also updating the weight values.
Let's have a look at how this is done in TripletConnection (starting from revision number 54dd8f36bc3f4a300b61cd60d93bd7fcee7a3b77 – 0.4.2 and onwards).
void TripletConnection::propagate_forward() { // loop over all spikes for (SpikeContainer::const_iterator spike = src->get_spikes()->begin() ; // spike = pre_spike spike != src->get_spikes()->end() ; ++spike ) { // loop over all postsynaptic partners for (const NeuronID * c = w->get_row_begin(*spike) ; c != w->get_row_end(*spike) ; ++c ) { // c = post index // transmit signal to target at postsynaptic neuron AurynWeight * weight = w->get_data_ptr( c ); transmit( *c , *weight ); // handle plasticity if ( stdp_active ) { // performs weight update *weight += dw_pre(*c); // clips too small weights if ( *weight < get_min_weight() ) *weight = get_min_weight(); } } } }
Here the outer for-loop runs over all spikes that arrive in the current time step. This is ensured by the calling the src→get_spikes() method. For a medium size network at moderately low firing rates and a standard integration time step size of dt=0.1ms, the number of spikes handled in this loop is usually relatively small (e.g. for 10000 neurons firing at 3Hz one would expect 1e4*3Hz*1e-4s=3 spikes on average).
The second nested loop (“loop over all postsynaptic partners”) for each spike *spike runs over all the postsynaptic partners *c which are stored the corresponding row in the weight matrix (an instance of the class SimpleMatrix).
What follows is a compact notation to get the synaptic weight from the matrix. AurynWeight * weight = w→get_data_ptr© gets a pointer to the data entry of the synaptic strength and stores it in value. Finally, the subsequent call of transmit( *c , *weight ); induces the postsynaptic conductance or PSC.
So far no plasticity has taken place, but we have merely described the mechanisms of spike propagation as it is also implemented in non-plastic connection objects (e.g. SparseConnection). All plasticity linked to presynaptic spiking happens next and, again for clarity, the important computation of the weight update takes place in dw_pre(*c) which I defined as follows
AurynWeight TripletConnection::dw_pre(NeuronID post) { // translate post id to local id on rank: translated_spike NeuronID translated_spike = dst->global2rank(post); AurynDouble dw = -hom_fudge*(tr_post->get(translated_spike)*get_hom(translated_spike)); return dw;
The code describes how each weight should be updated upon a presynaptic spike (hence the suffix). Since spikes in Auryn are labeled with the global id of a neuron within a SpikingGroup, we need to translate this to the local ID, i.e. the index of the neuron on that rank. This is done by the function global2rank. Next, we compute the weight update. In the minimal triplet STDP model by Pfister and Gerstner (2006) which is implemented in TripletConnection a presynaptic spike causes LTD. The amount of LTD is proportional to one of the postsynaptic traces tr_post. Moreover, the amount of LTD is homeostatically modulated by a factor derived from a slower trace (get_hom(translated_spike)). Finally hom_fudge is a factor which contains the learning rate and a normalization constant for the value returned by get_hom. By precomputing this product, we save a few multiplications each time this function is called.
The complete weight update dw is ultimately returned to our propagate_forward() function where it is added to the weight value.
One thing you should pay close attention to, because it could might easily introduce errors: You need to translate postsynaptic IDs (as shown above), but not the presynaptic ones! Copies of presynaptic trances are available on each rank, whereas postsynaptic traces are distributed with the neuronal dynamics. This only makes a difference when you are running simulations in parallel with MPI, but then it's an important difference.
We now covered weight updates triggered by presynaptic spikes, but what happens upon a postsynaptic spike?
Backward spike propagation
For this case plastic connections inherit from DuplexConnection. An instance of DuplexConnection implements the functionality to efficiently read all presynaptic partners of a neuron. It is build upon finalization of each connection object from the weight matrix w (the “forward matrix”) and contains pointers to the actual weight values. All back propagating action potentials are handled in the function propagate_backward():
void TripletConnection::propagate_backward() { if (stdp_active) { SpikeContainer::const_iterator spikes_end = dst->get_spikes_immediate()->end(); // loop over all spikes for (SpikeContainer::const_iterator spike = dst->get_spikes_immediate()->begin() ; // spike = post_spike spike != spikes_end ; ++spike ) { // Since we need the local id of the postsynaptic neuron that spiked // multiple times, we translate it here: NeuronID translated_spike = dst->global2rank(*spike); // loop over all presynaptic partners for (const NeuronID * c = bkw->get_row_begin(*spike) ; c != bkw->get_row_end(*spike) ; ++c ) { #ifdef CODE_ACTIVATE_PREFETCHING_INTRINSICS // prefetches next memory cells to reduce number of last-level cache misses _mm_prefetch((const char *)bkw_data[c-bkw_ind+2], _MM_HINT_NTA); #endif // computes plasticity update AurynWeight * weight = bkw->get_data(c); *weight += dw_post(*c,translated_spike); // clips too large weights if (*weight>get_max_weight()) *weight=get_max_weight(); } } } }
Again the magic happens in dw_post(NeuronID pre, NeuronID post) which computes the weight update as follows:
AurynWeight TripletConnection::dw_post(NeuronID pre, NeuronID post) { // at this point post was already translated to a local id in // the propagate_backward function below. AurynDouble dw = A3_plus*tr_pre->get(pre)*tr_post2->get(post); return dw; }
If you are familiar with the minimal Triplet STDP model by Pfister and Gerstner (2006), you will recognize the LTP term in the function which is derived from multiplying two traces together. For the experts, it is important to note that Auryn updates traces after updating all the weights (i.e. the -epsilon of the time argument to the postsynaptic trace is therefore implicit). The standard doublet STDP would only have the pre-trace (tr_pre) here instead. The expression should be otherwise quite self-explanatory.
In both cases (forward and backward propagation) the weight updates are followed by some weight clipping to enforce certain weight bounds (for instance to obey Dale's law).
Changing the plasticity model
Most of the plasticity models in Auryn follow the design principles introduced above (e.g. http://fzenke.net/auryn/doxygen/current/classauryn_1_1STDPConnection.html). Suppose, you would like to change the plasticity model, all you need to do is to copy TripletConnection.h and TripletConnection.cpp to YourNameConnection.h and .cpp and then the dw_pre and dw_post would be the first places start to change things. Of course you can declare new parameters in the header of the Connection object and either directly set them from the main program, hard code them 
dw_pre and dw_post altogether. For instance if you would like to implement a weight dependence, you will need to include our above *weight variable into the parameter list of these functions. Similarly, you might want to access the postsynaptic membrane voltage through dst→get_mem(NeuronID id) and pass it to you dw functions … I will let you experiment and hope that I will have the time to include some more examples here soon.
Weight updates in continuous time (evolve)
To implement time continuous updates it is possible to overwrite the virtual function evolve() which is called each time step. Similar to the evolve function of a NeuronGroup, it is meant to do a one step integration of the differential equations describing the weight dynamics. However, you can do anything in this function really.
Let me give a simple example. For instance, the following code lets you iterate over all weights:
void TripletConnection::evolve() { for (AurynLong i = 0 ; i < w->get_nonzero() ; ++i ) { AurynWeight * weight = w->get_data(i); // do something with the weight } }
which could for instance be used to implement a weight decay. Note, that you will have to declare the function in the header file first. Another word of warning is in order here. Since there are typically many weights, updating all of them in every time step will result in slow simulations. If your learning rule requires such an update, you have to go with it and gain speed through parallelization. In some situations it helps if the process you are modelling is much slower than the weight dynamics driven by spikes. For instance, if you want to implement synaptic scaling on plausible time scales, you can choose a larger integration time step for you weights. A simple way to achieve this would be the following code:
if ( sys->get_clock()%timestep_scaling == 0 && stdp_active ) { for (AurynLong i = 0 ; i < w->get_nonzero() ; ++i ) { AurynWeight * weight = w->get_data_ptr(i); // do something with the weight } } }
where you will have to define and initialize the variable time_scaling somewhere in your connection object. It will give you the new step width in multiples of Auryn's time step dt.
This should give you the necessary tools to start out with writing your own plasticity models. As with all code, write simple unit tests to ensure you are simulating what you want to simulate. Happy coding.